Почему пакет программ статистического анализа
1. Почему пакет программ статистического анализа нельзя считать программой искусственного интеллекта?
2. Могут ли психологи подсказать нам, как сконструировать думающую машину?
3. Как вы понимаете термин "пространство поиска"? Что представляет собой пространство поиска в игре в шахматы?
4. Как вы понимаете термин "пространство решений"? Что представляет собой пространство решений в игре в шахматы?
5. Ниже приведен алгоритм поиска в глубину. Он записан с помощью функциональной нотации, которая подчеркивает его рекурсивную структуру. Таким образом, dfs представляет собой функцию трех аргументов: goal, current и pending:
(а b с) + (d e f ) = (а b с d e f);
first(a b с) = a
rest(a b c) = (b c).
I) Выразите следующий алгоритм на каком-либо из известных вам языков программирования.
dfsfgoal, current, pending)
{
if current = goal, then success;
else
{
pending := expand (current}+ pending;
if pending = () then fail;
else dfs(goal, first(pending), .rest( pending));
} }
II) Разработайте аналогичный алгоритм для поиска в ширину и реализуйте его на том же языке. Необходимо будет изменить только одно выражение в функции dfs.
6. Рассмотрите головоломку "миссионеры и каннибалы", схематически представленную на рис. 2.6.
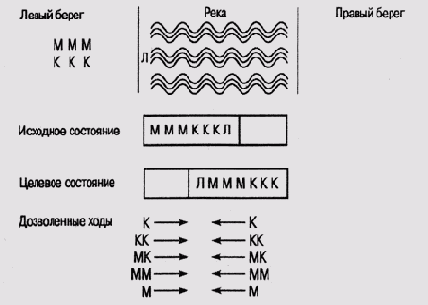
Рис. 2.6. Головоломка "миссионеры и каннибалы "
Условия головоломки следующие.
На левом берегу реки находятся три миссионера и три каннибала. К этому же берегу причалена единственная лодка. На этой лодке нужно переправить всех миссионеров и всех каннибалов на правый берег при условии, что лодка одновременно может перевозить не более двоих, в обратный путь на лодке должен отправиться хотя бы один человек.
Таким образом, дозволены следующие варианты шагов (переправ):
К-> одного каннибала с левого берега на правый
КК-> двух каннибалов с левого берега на правый
МК-> одного миссионера и одного каннибала с левого берега на правый
ММ-> двух миссионеров с левого берега на правый
М-> одного миссионера с левого берега на правый
К этому нужно добавить такие же варианты переправы с правого берега на левый. Но есть еще одно обстоятельство, существенно влияющее на весь процесс: если окажется, что каннибалов на любом из берегов больше, чем миссионеров, то несчастных просто съедят. Решение головоломки — это последовательность шагов с учетом описанных ограничений, переводящая систему в заданное конечное состояние.
Конечно, эту головоломку можно решить и простым перебором и испытанием всех возможных состояний, поскольку пространство поиска не так уж велико. На рис. 2.7 показано, как образуется пространство поиска рекурсивным применением дозволенных операторов, причем на графе состояний особо выделены узлы, приводящие к образованию петель, и узлы, соответствующие недозволенным состояниям (когда кто-либо из миссионеров обречен).
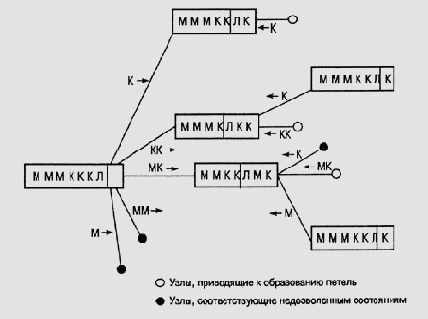
Рис. 2.7. Построение пространства поиска в головоломке "миссионеры и каннибалы"
На рис. 2.8 показано законченное пространство поиска, сформированное алгоритмом поиска в глубину, причем перебор возможных шагов ведется в том порядке, в котором они перечислены в представленном в условии, списке.
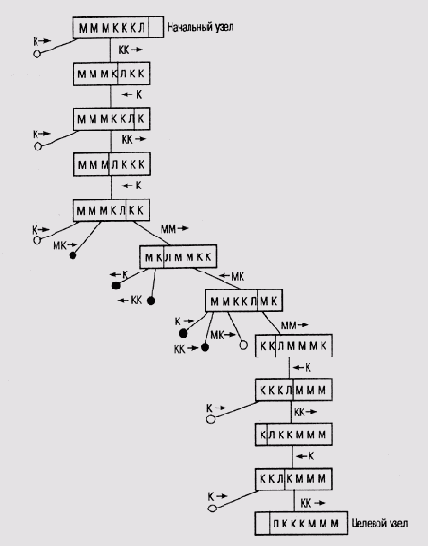
Рис. 2.8. Законченное пространство поиска в головоломке "миссионеры и каннибалы ", сформированное алгоритмом поиска в глубину
В процессе поиска было развернуто 22 узла, а путь, приводящий к успеху, содержит 11 узлов. Таким образом, оценка проницательности поиска равна 11/22=0.5. Грубо говоря, проницательность поиска говорит нам о том, насколько данный алгоритм позволил избежать выполнения ненужной работы в процессе Поиска решения. Чем выше значение проницательности поиска для того или иного алгоритма, тем лучше.
I) Выберите представление состояний на берегах реки и разработайте программу, которая решает эту задачу, используя оба варианта алгоритмов поиска— в глубину и в ширину.
С разными способами формализации этой
задачи можно познакомиться в работе Амарела [Amarel, 1968]. Обратите внимание на то, что существуют способы представления состояний, которые позволяют более экономно использовать вычислительные ресурсы при решении задачи.
II) Попытайтесь улучшить оценку проницательности поиска, полученную для алгоритма поиска в глубину (рис. 2.8), изменив порядок, в котором анализируются в каждом очередном состоянии дозволенные операторы.
III) Обобщите программу как в части количества пассажиров в лодке, так и в части количества миссионеров/каннибалов. Сделайте их параметрами программы, задаваемыми извне. Если вы начнете проводить эксперименты с такой программой, то убедитесь, что, во-первых, эти параметры нельзя варьировать независимо, поскольку при некоторых комбинациях задача не имеет решения, а во-вторых, увеличение значений любого из параметров существенно расширяет пространство поиска.
7. Другая классическая головоломка, знакомая в несколько ином виде многим еще со школьной скамьи, — "Восьмерка". В головоломке принимает участие восемь пронумерованных фишек, которые могут перемещаться по игровому полю 3x3. Цель состоит в том, чтобы из некоторого случайного расположения фишек перейти к упорядоченному (рис. 2.9).
Мы несколько модифицируем ограничения, сформулировав их в терминах перемещения единственного "пустого поля".
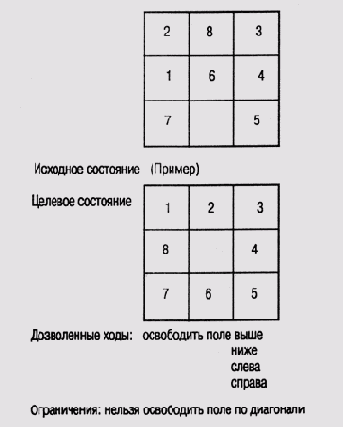
Рис. 2.9. Головоломка "Восьмерка"
В отличие от задачи о миссионерах и каннибалах, эту головоломку можно решить за приемлемое время методом "слепого" поиска. Дело в том, что головоломка имеет только 9! состояний и, следовательно, можно использовать для поиска очередного хода оценочную функцию по методике "восхождения на гору".
I) Придумайте оценочную функцию для этой задачи и разработайте программу, которая реализует поиск по методике "восхождения на гору". Возможные варианты оценочной функции некоторого состояния должны включать, во-первых, количество фишек, которые стоят не на своих местах, а во-вторых, сумму расстояний от текущего положения каждой фишки до предназначенного ей целевого (имеются в виду расстояния по Евклиду).
II) Какая из предложенных выше оценочных функций является более чувствительной? Можете ли вы предложить лучший способ управления поиском?
III) Как будет работать ваша программа, если увеличить количество фишек до 15, а размер игрового поля до 4x4? В этом случае придется исследовать 16! состояний.
Эту головоломку с точки зрения методов искусственного интеллекта рассматривал Нильсон (см. [Nilsson, 1980, Chapter 1].
8. Просмотрите описание алгоритма А во врезке 2.2 и выполните следующее.
I) Реализуйте алгоритм А на любом известном вам языке программирования.
II) С помощью созданной программы попробуйте решить головоломки "о миссионерах и каннибалах" и "Восьмерку". (Придется придумать оценочную функцию для головоломки "о миссионерах и каннибалах". Воспользуйтесь оценочной функцией из упр. 7.)
III) Попробуйте с помощью этого алгоритма решить криптоарифметическую головоломку, описанную ниже:
BEST |
SEND |
DONALD |
CROSS |
||
+MADE |
+MORE |
+GERALD |
+ROADS |
||
MASTER |
MONEY |
ROBERT |
DANGER |
||
Термин "криптоарифметическая" означает использование цифр, зашифрованных буквами, и соответственно чисел, зашифрованных словами. Задача состоит в том, чтобы найти, какие цифры нужно подставить вместо букв, чтобы представленные арифметические операции над расшифрованными числами давали верный результат. Такая задача рассматривается во многих классических работах по искусственному интеллекту (см., например, [Raphael, 1976, Chapter 3].
Вам придется подумать над тем, как представить слагаемые и сумму, какие возможны в решении этой задачи "ходы" (т.е. какой набор операций можно предложить для перехода из одного состояния в другое) и какую эвристику можно применить для управления поиском.