Пересмотр теорий высказываний
Систему отслеживания истинности предположений, разработанную Мак-Аллестером [McAllester, 1980], нельзя отнести к самым первым, но ее, пожалуй, лучше всего использовать в качестве наглядного пособия. Использованный им метод пересмотра предполагает наличие в системе базы данных утверждений, в которой пользователь может квалифицировать формулы как "истинные", "ложные" или "неопределенные". Таким образом, в основе метода лежит трехзначная логика, в отличие от классической двузначной, которую мы рассматривали в главе 8. Система представляет утверждения в виде узлов, которые хранят соответствующие значения.
Ограничения, которые накладывает на содержимое базы данных утверждений система отслеживания истинности, представляют собой фундаментальные аксиомы логики высказываний. Например, аксиома
¬(U^¬U)
утверждает, что высказывание U может быть одновременно и истинным, и ложным. (Учтите, что -U является метапеременной, которая представляет любое высказывание.) Система отслеживания истинности предположений, разработанная Мак-Аллестером, как и большинство других подобных систем, имеет дело только с формулами, которые не содержат кванторов. Например, в теорию может входить высказывание DEAD(fred), но не может входить (любой X)(DEAD(X)). Это ограничение существует по той простой причине, что не всегда возможно установить совместимость теории первого порядка, как это отмечалось в главе 8.
Система отслеживания истинности выполняет по отношению к базе данных четыре функции.
(1) Реализует множество дедукций высказываний, которые Мак-Аллестер назвал распространением пропозициональных принуждений (propositional constraint propagation).
(2) Формирует обоснования при присвоении высказываниям значений истинности, когда такое присвоение выполняется в результате распространения принуждений (а не при установке значения пользователем). Таким образом, если мы приходим к заключению, что q истинно, поскольку истинны p и (p


(3) Обновляет базу данных утверждений, как только какое-либо высказывание удаляется. Так, если мы приходим к выводу, что q истинно, поскольку истинны р и (p


(4) Отслеживает цепочку предположений, которые привели к противоречию, с помощью метода, получившего наименование обратное прослеживание, ведомое зависимостями (dependency-directed backtracking). После этого пользователю предлагается удалить одно из предположений, "виновных" в появлении противоречия.
Задавшись предположениями р и (— p v q) и пользуясь механизмом распространения принуждений, система отслеживания истинности может получить q. Затем она формирует поддерживающую структуру, представленную на рис. 19.2. Каждый узел в этой сети представляет собой фрейм (см. о фреймах в главе 6) с набором слотов, один из которых хранит наименование узла, другой — значение истинности, а третий — указатель на обоснование. Обоснование представлено другим фреймом, который содержит таблицу поддерживающих высказываний и их значения истинности. В структуре на рис. 19.2 истинность узла q подтверждается тем фактом, что узлы, представляющие р и (— p v g), отмечены как имеющие значения "истина". Обратите внимание на то, что узлы, представляющие предположения, как, например, р, не имеют указателей на фреймы обоснования, поскольку они полагаются истинными по определению.
Если в дальнейшем окажется, что значение q несовместимо с содержимым остальной базы данных утверждений, то, анализируя описанную структуру данных, можно будет выйти на фреймы обоснования. После этого пользователю будет предоставлена возможность проследить цепочку зависимостей, связанную либо с р, либо с (-p v q). Для выполнения такого отслеживания очень важно, чтобы структуры поддержки были убедительными.Убедительность структуры означает отсутствие зацикливания, т.е. отсутствие такой ситуации, когда некоторое высказывание не подтверждает через "посредников" само себя.
Обратите внимание — все утверждения являются либо предположениями, введенными пользователем, либо обосновываются наличием других утверждений. В следующем разделе мы рассмотрим другую, более сложную систему отслеживания истинности предположений, в которой допускается использовать в качестве обоснования отсутствие запрещающей информации.
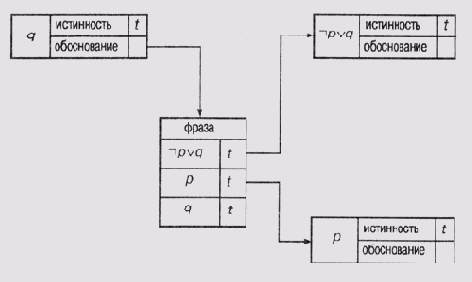
Рис. 19.2. Структура представления связей между высказываниями
